Viscosity, Viscous force and Coefficient of Viscosity

Definition of Viscosity:

It is the property of a fluid that opposes the relative motion between its adjacent layers. This property of the fluid is known as viscosity. It is also called the resistance of fluid to flow or deformation or fluid thickness.

Effect of temperature on Viscosity:

The viscosity of the fluid decreases sharply with the temperature rise and becomes zero at boiling temperature. On the other hand, the viscosity of the gases increases with the temperature rise.

Definition of Viscous Force (Internal Frictional Force):

When a layer of fluid slide over another layer of the same fluid then an internal tangential frictional force act between them which opposes the relative motion between the layers. This tangential force is called viscous force or internal frictional force.

In the absence of external force, the viscous force would soon bring the fluid to rest.

Factor affecting the viscous force:

There are the following factors that affect the viscous force-

1.) The viscous force is directly proportional to the contact area of the layers. i.e.

$F \propto A \qquad(1)$

Where $A \rightarrow$ The contact area of the layers

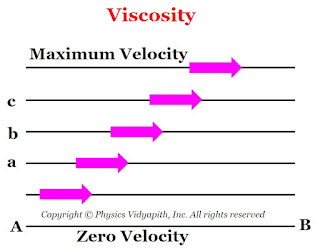
2.) The viscous force is directly proportional to the velocity gradient between the layers. i.e.

$F \propto \frac{\Delta v_{x}}{\Delta z} \qquad(2)$

Where $\frac{\Delta v_{x}}{\Delta z} \rightarrow$ The velocity gradient that is shown in the figure below

From equation $(1)$ and equation $(2)$

$F \propto A \: \frac{\Delta v_{x}}{\Delta z}$

$F = \pm \: \eta \: A \: \frac{\Delta v_{x}}{\Delta z} \qquad(3)$

Where

$\eta \rightarrow$ It is a constant and also known as the "coefficient of viscosity" of the fluid.

$ \pm \rightarrow$ It indicates that the viscous force $F$ between two layers of fluid is a mutually interacting force. As shown above in figure (B), A layer that is just above layer $A$ exerts a force in the forward direction while a layer that is just below layer $A$ exerts an equal and opposite force i.e. in the backward direction.

Definition of Coefficient of Viscosity:

If $A=1$ and $\frac{\Delta v_{x}}{\Delta z} = 1$, then from equation $(3)$

$\eta = 1$

So from the above equation,  If the contact area and velocity gradient are units then the viscous force between the fluid is known as the coefficient of velocity.

Dimension of coefficient of viscosity:

$\left[ M L^{-1} T^{-1} \right]$

Unit of coefficient of viscosity:

$Kg-m^{-1}s^{-1}$

Here

$1 \: Kg-m^{-1}s^{-1} = 10\: poise = 1 \: decapoise$