Combined Focal Length and Power of two thin lenses in contact
Derivation of the combined focal length and power of two thin lenses in contact:
Case (1): When both are convex lens-
a.) The combined focal length of two thin convex lenses in contact:
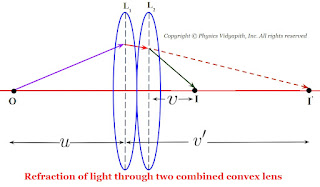
Let us consider that two convex lenses $L_{1}$ and $L_{2}$ are connected with transparent cement Canada Balsam. If the focal length of the lenses is $f_{1}$ and $f_{1}$ and an object $O$ is placed at distance $u$ from the first lens $L_{1}$ and its image $I'$ is formed at a distance $v'$ from the first lens $L_{1}$. Therefore from the equation of focal length for lens $L_{1}$
$\frac{1}{f_{1}} = \frac{1}{v'} - \frac{1}{u} \qquad(1)$
For the second lens, The image $I'$ works as a virtual object for the second lens $L_{2}$ which image $I$ is formed at a distance $v$ from the second lens $L_{2}$. Therefore from the equation of focal length for lens $L_{2}$
$\frac{1}{f_{2}} = \frac{1}{v} - \frac{1}{v'} \qquad(2)$
Now add the equation $(1)$ and equation $(2)$. then
$\frac{1}{f_{1}} + \frac{1}{f_{2}} = \frac{1}{v'} - \frac{1}{u} + \frac{1}{v} - \frac{1}{v'} $
$\frac{1}{f_{1}} + \frac{1}{f_{2}} = \frac{1}{v} - \frac{1}{u} $
Where $ \frac{1}{f} = \frac{1}{v} - \frac{1}{u} $
$\frac{1}{f_{1}} + \frac{1}{f_{2}} = \frac{1}{f} \qquad(3)$
$\frac{1}{f} = \frac{f_{1} + f_{2}}{f_{1}f_{2}} $
$f = \frac{f_{1}f_{2}}{f_{1} + f_{2}} $
This is the equation of the combined focal length of two thin convex lenses in contact.
b.)The combined power of two thin convex lenses in contact:
We know that the power of the lens equation
$P = \frac{1}{f}$
So from equation $(3)$
$P=P_{1} + P_{2}$
This is the equation of the combined power of two thin convex lenses in contact.
Similarly for another two cases $(2)$ and case $(3)$:
Case (2): When both are concave lens-
a.) The combined focal length of two thin concave lenses in contact:
For concave lenses the focal length for both lenses i.e. ($f_{1} \: and \: f_{2}$) will be negative. Therefore the combined focal length of the two thin concave lens
$ \frac{1}{f} = \frac{1}{- f_{1}} + \frac{1}{- f_{2}} $
$\frac{1}{f} =- \frac{\left(f_{1} + f_{2} \right)}{f_{1}f_{2}} $
$f = -\frac{f_{1}f_{2}}{f_{1} + f_{2}} $
b.) The combined power of two thin concave lenses in contact:
$P= - \left(P_{1} + P_{2}\right)$
Case (3): When one lens is convex and the second is concave-
a.) The combined focal length of two thin lenses for convex and concave:
If the focal length of convex lens is $f_{1}$ and for concave is $f_{2}$ then the combine focal length of lenses
$ \frac{1}{f} = \frac{1}{ f_{1}} + \frac{1}{- f_{2}} $
$\frac{1}{f} = \frac{\left(f_{1} - f_{2} \right)}{f_{1}f_{2}} $
$f = \frac{f_{1}f_{2}}{f_{1} - f_{2}} $
b.) The combined power of two thin lenses for convex and concave:
$P= \left(P_{1} - P_{2}\right)$