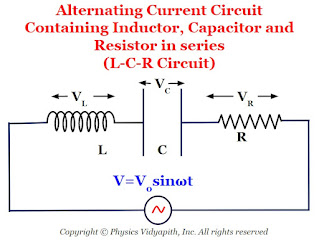
Circuit containing Inductor, Capacitor, and Resistor in Series (L-C-R Series Circuit )
Mathematical Analysis of L-C-R Series Circuit :
Let us consider, a circuit containing inductor $L$, capacitor $C$, and resistor $R$ and these are connected in series. If an alternating voltage source is applied across it then the resultant voltage of the L-C-R circuit
$V=\sqrt{\left( V_{L} -V_{C} \right)^{2} + V^{2}_{R}} \qquad(1)$
We know that:
$V_{R} = iR$
$V_{L} = iX_{L}$
$V_{C} = iX_{C}$
So from equation $(1)$
$V=\sqrt{\left( iX_{L} - iX_{C} \right)^{2} + (iR)^{2}} $
$V=i\sqrt{\left( X_{L} - X_{C} \right)^{2} + R^{2}} $
$\frac{V}{i}=\sqrt{\left( X_{L} - X_{C} \right)^{2} + R^{2}} $
$Z=\sqrt{\left( X_{L} - X_{C} \right)^{2} + R^{2}} \qquad(2)$
Where
$Z \rightarrow$ Impedance of L-C-R circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
$X_{C} \rightarrow$ Inductive Reactance which has value $\frac{1}{\omega C}$
So from equation $(2)$, we get
$Z=\sqrt{\left( \omega L - \frac{1}{\omega C} \right)^{2} + R^{2}} \qquad(3)$
The phase of resultant voltage:
If the phase of resultant voltage from from current is $\phi$ then
$tan \phi = \frac{X_{L} - X_{C}}{R} \qquad(4)$
$tan \phi = \frac{\omega L - \frac{1}{\omega C}}{R} $
$ \phi = tan^{-1} \left( \frac{\omega L - \frac{1}{\omega C}}{R} \right) $
The Impedance and Phase at Resonance Condition:($X_{L} = X_{C}$):
At resonance $X_{L} = X_{C} \qquad(5)$
$\omega L = \frac{1}{\omega C}$
$\omega^{2} = \frac{1}{L C}$
$\omega = \sqrt{\frac{1}{L C}}$
$2 \pi f = \sqrt{\frac{1}{L C}}$
$ f = \frac{1}{2 \pi}\sqrt{\frac{1}{L C}}$
Where $f \rightarrow$ Natural frequency of the circuit
1.) The Impedance of the circuit at resonance condition:
Substitute the resonance condition i.e. $X_{L} = X_{C}$ in equation $(2)$ then the impedance of the L-C-R Circuit
$Z=R$
The impedance of the L-C-R circuit at resonance condition is equal to the resistance of the resistor applied in a circuit.
2.) The Phase of resultant voltage at resonance condition:
$tan\phi =0$
$tan\phi = tan 0^{\circ}$
$\phi=0^{\circ}$
The phase of resultant voltage at resonance condition is zero. i.e. the direction of resultant voltage in the direction of current in the circuit.
Note: There are following cases arise in the L-C-R circuit at resonance condition
Case -1:
If $X_{L} \gt X_{C}$, the $tan \phi$ is positive, i.e. $\phi$ is positive. In this case, the voltage leads to the current. Therefore, the circuit is more inductive rather than capacitive or resistive.
Case -2:
If $X_{L} \lt X_{C}$, the $tan \phi$ is negative, i.e. $\phi$ is negative. In this case, the voltage lags behind the current. Therefore, the circuit has a more capacitance-dominated circuit.
Case -3:
If $X_{L} = X_{C}$, the $tan \phi$ is zero, i.e. $\phi$ is negative. In this case, the voltage and the current are in phase. Therefore, the circuit is purely resistive.
$V_{L} = iX_{L}$
$V_{C} = iX_{C}$
$Z \rightarrow$ Impedance of L-C-R circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
$X_{C} \rightarrow$ Inductive Reactance which has value $\frac{1}{\omega C}$