Bohr's Model of Atom

Bohr's Atomic Model Postulates:

Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:

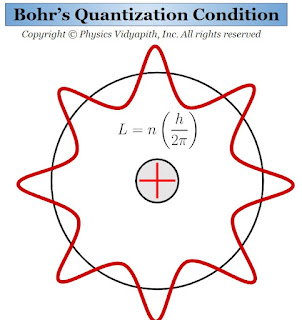
1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,

$mvr=\frac{nh}{2\pi}$

Where $h$ is Planck's universal constant

This Bohr's equation is called the "Bohr's quantization Condition"

2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.

3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".

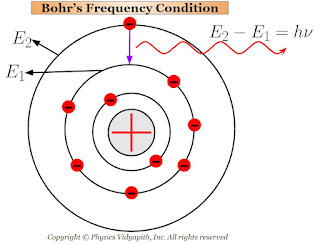
The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.

This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:

$E=E_{2} - E_{1}$

$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$

$\nu=\frac{E_{2} - E_{1}}{h}$

This Bohr's equation is called the "Bohr's frequency condition".