Torque on an electric dipole in a uniform electric field: Let us consider, An electric dipole AB, made up of two charges $+q$ and $-q$, is placed at a very small distance $2l$ in a uniform electric field $\overrightarrow{E}$. If $\theta$ is the angle between electric field intensity $\overrightarrow{E}$ and electric dipole moment $\overrightarrow{p}$ then the magnitude of electric dipole moment →
$\overrightarrow{p}=q\times\overrightarrow{2l}\qquad(1)$
Force exerted on charge $+q$ by electric field $\overrightarrow{E}$ →
$\overrightarrow{F_{+q}}=q\overrightarrow{E}\qquad(2)$
Here in the above equation(2), the direction of $\overrightarrow{F_{+q}}$ is along the direction of $\overrightarrow{E}$
Force exerted on charge $-q$ by electric field $\overrightarrow{E}$ →
$\overrightarrow{F_{-q}}= q\overrightarrow{E}\qquad(3)$
Here in the above equation(3) the direction of $\overrightarrow{F_{-q}}$ is in the opposite direction of $\overrightarrow{E}$
So, the net force of on an electric dipole→
$\overrightarrow{F}=\overrightarrow{F_{+q}} - \overrightarrow{F_{-q}}\qquad (4)$
Now substitute the value of equation $(2)$ and equation $(3)$ in above equation $(4)$. So net force→
$\overrightarrow{F}=0\qquad (5)$

|
|
Torque on electric dipole
|
Hence, the net translating force on an electric dipole in a uniform electric field is zero. But these two force is equal in magnitude, opposite in
direction, and act at different point of the dipole so these force form a coupling force that exerts a torque on an electric dipole→
Torque = force x Perpendicular distance between the two forces
$\overrightarrow{\tau}=(qE).2l\:sin\theta\quad\quad\quad\quad(6)$
$ \overrightarrow{\tau}=pE\:sin\theta$
$\overrightarrow{\tau}=\overrightarrow{p}\times\overrightarrow{E}$
Case(I)→ If the dipole is placed perpendicular to the electric field i.e. $\theta=90^{\circ}$, the torque acting on it will be maximum. i.e.
$ \tau_{max}=pE $
Case(II)→ If the dipole is placed parallel to the electric field i.e. $\theta=0^{\circ}$ or
$\theta=180^{\circ}$, the torque acting on it will be minimum. i.e.
$ \tau_{min}=0$

|
|
Direction of torque
|
Electric Dipole Moment:
We know that the torque
$ \overrightarrow{\tau}=pE\:sin\theta$
If $E=1$ and $\theta=90^{\circ}$ Then
$ \tau_{max} =p$
Hence Electric dipole moment is the torque acting on the dipole placed perpendicular to the direction of uniform electric field intensity.
Torque on an electric dipole in a non-uniform electric field:
In a non-uniform electric field, the $+q$ and $-q$ charges of a dipole experience different forces (not equal in magnitude and opposite in direction) at a slightly different position in the electric field, and hence a net force $\overrightarrow{F}$ act on the dipole in a non-uniform field. A net torque acts on the dipole which depends on the location of the dipole in the non-uniform field.
$\overrightarrow{\tau}=\overrightarrow{p}\times\overrightarrow{E}(\overrightarrow{r})$
Where $\overrightarrow{r}$ is the position vector of the center of the dipole.

|
|
When p and E are Parallel
|
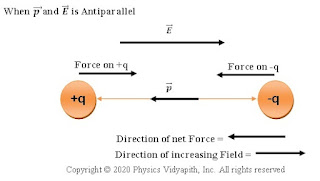
In the non-uniform field, If the direction of the dipole moment $\overrightarrow{p}$ is parallel to electric field intensity $\overrightarrow{E}$ or antiparallel to electric field intensity $\overrightarrow{E}$ the net torque on the dipole is zero because the force on charges becomes linear.
 |
|
When p and E are antiparallel
|
However, If $\overrightarrow{p}$ is parallel to $\overrightarrow{E}$, a net force on the dipole in the direction of increasing $\overrightarrow{E}$. When $\overrightarrow{p}$ is antiparallel to $\overrightarrow{E}$, a net force on the dipole in the direction of decreasing $\overrightarrow{E}$. As shown in the figure above.





