Motion of body in a vertical circle and its Practical Applications

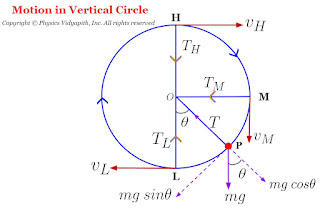
Calculation of Motion of a body in a vertical Circle: Let us consider, A body that has mass $m$ moving in a vertical circle of radius $r$. If at any instant the body is at position $P$ with angular displacement $\theta$ from the lower position $L$ of the circle. As shown in the figure below.

The various forces acting on the body are:

The weight $mg$ of the body, acting vertically downwards

Tension $T$in the string acting along the $PO$. Now $mg$ can be resolved into two components:

1.) The horizontal component $mg cos\theta$ opposite to $T$

2.) The vertical component $mg sin\theta$ act along tangent to the circle at $P$

So the net force on the body at position $P$ provides the necessary centripetal force required by the body

$T-mg cos\theta = \frac{m v^{2}}{r}$

$T= \frac{m v^{2}}{r} + mg \: cos\theta \qquad(1)$

Tension and velocity at the highest position $H$ of the verticle circle: At the highest position $H$ the tension $T_{H}$ of the will be minimum and the velocity $v_{H}$ will also be minimum.

If $cos\theta = -1$ i.e. $\theta=180^{\circ}$

Then Tension $T$ and velocity $v$ will be minimum i.e $T_{H}$ and $v_{H}$

so from equation $(1)$

$T_{H}= \frac{m v_{H}^{2}}{r} - mg $

So from the above equation, we can conclude that The body will move along the vertical circle only when $T_{H} \geq 0$

$\left( \frac{m v_{H}^{2}}{r} - mg \right) \geq 0$

$ \frac{m v_{H}^{2}}{r} \geq mg $

$ \frac{ v_{H}^{2}}{r} \geq g $

$ v_{H} \geq \sqrt {rg} $

Thus the minimum value of the velocity at the highest position is $\sqrt{rg}$

Tension and velocity at lowest position $L$ of the verticle circle: At the lowest position $L$ the tension and velocity will be maximum. Now applying the principle of energy conservation for the position $H$ and $L$ of the body.

Total energy at $L$ =Total energy at $H$

$\frac{1}{2}m v_{L}^{2}=\frac{1}{2}m v_{H}^{2} +mg(2r)$

Now substitute the value of $v_{H} \geq \sqrt{gr}$ in above equation then we get

$\frac{1}{2}m v_{L}^{2}=\frac{1}{2}m (gr) +mg(2r)$

$\frac{1}{2}m v_{L}^{2}=\frac{5mgr}{2}$

$v_{L} \geq \sqrt{5gr}$

For the maximum value of tension $T_{L}$ at the lowest position $L$ of the vertical circle. Now put $cos \theta =1$ i.e $\theta=0^{\circ}$ in the equation $(1)$ then we get

$T_{L}= \frac{m v_{L}^{2}}{r} + mg $

Now substitute the value of $v_{L} \geq \sqrt{5gr}$ in the above equation then

$T_{L} \geq \frac{m 5gr}{r} + mg $

$T_{L} \geq 6gr$

Tension and velocity at horizontal position $M$ of the verticle circle:

Now apply the principle of conservation of energy for position $M$ and position $L$

Total energy at $M$ =Total energy at $L$

$ \frac{1}{2}m v_{M}^{2} + mgr = \frac{1}{2} m v_{L}^{2}$

$ \frac{1}{2}m v_{M}^{2} = \frac{1}{2} m v_{L}^{2} - mgr$

Now substitute the value of $v_{L} \geq \sqrt{5gr}$ in the above equation then

$ \frac{1}{2}m v_{M}^{2} \geq \frac{1}{2} m 5gr - mgr$

$ \frac{1}{2}m v_{M}^{2} \geq \frac{3 mgr}{2}$

$v_{M}^{2} \geq 3 gr$

$v_{M} \geq \sqrt{3 gr}$

To find the tension $T_{M}$ at position $M$ substitute the $cos \theta =0$ i.e $\theta =90^{\circ}$ in equation $(1)$. Then we get

$T_{M} = \frac{m v_{M}^{2}}{r} + 0$

$T_{M} = \frac{m v_{M}^{2}}{r}$

Now substitute the value of $v_{M} \geq \sqrt{3gr}$ in the above equation. Then we get

$T_{M} \geq 3mg$

Practical Application of motion in a vertical Circle:

1.) When a bucket containing water is rotated in a vertical circle with a velocity at the lowest point $v_{L} \geq \sqrt{5gr}$, water shall not spill even at the highest point, when the bucket is upside down. If the bucket is whirled slowly, so that $ \left(mg \gt \frac{mv_{H}^{2}}{r} \right) $, then a part of the weight shall provide the necessary centripetal force $\left( \frac{mv_{H}^{2}}{r} \right)$; and the rest of the weight of water $\left( mg - \frac{mv_{H}^{2}}{r} \right) $ causes some water to accelerate downwards and spill. Only this much water shall leave the bucket.

2.) A pilot of an aircraft can successfully loop a vertical loop without falling at the top of the loop (being without a belt) when its velocity at the bottom of the loop is $\geq \sqrt{5gr}$

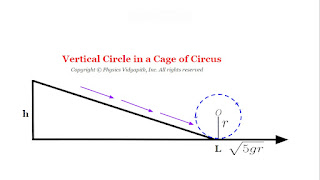
3.) In a circus, a motorcyclist is able to perform the feat of driving the motorcycle along a vertical circle in a cage. The motorcyclist does not fall even at the highest point, when his velocity at the bottom of the cage is $\geq \sqrt{5gr}$.

To acquire this velocity at the lowest point $L$ of the vertical circle of radius $r$, he has to roll down a vertical height $h$, As shown in the figure below:

From the equation of motion $v^{2}=u^{2}+2as$

Let $u=0$, $a=+g$ and $s=h$

we get, $v^{2}=0 +2gh$

$v=\sqrt{2gh}$

To move in a vertical circle, the velocity $v$ acquired at $L$ must at least be equal to $\sqrt{5gr}$. i.e.

$\sqrt{2gh}= \sqrt{5gr}$

$h=\frac{5r}{2}$