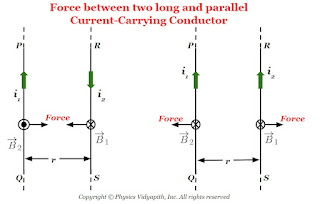
Derivation of Force between two long and parallel current-carrying conductors:
Let us consider:
The two long straight, parallel conductors = $PQ$ and $RS$
The length of the conductor= $l$
The distance between the parallel conductor = $r$
The current flowing in conductor $PQ$ = $i_{1}$
The current flowing in conductor $RS$ = $i_{2}$
The magnetic field due to conductor $PQ$ = $B_{1}$
The magnetic field due to conductor $RS$ = $B_{2}$
The magnetic force on conductor $PQ$= $F_{1}$
The magnetic force on conductor $RS$= $F_{2}$
 |
| Force Between Parallel Current Carrying Conductor |
Now Consider the magnetic force on conductor $RS$ is i.e.
$F_{2}=i_{2}B_{1}l sin\theta$
Where $\theta$ is the angle between the magnetic field and length element of conductor i.e. $\theta=90^{\circ}$ so above equation can be written as,
$F_{2}=i_{2}B_{1}l sin 90^{\circ}$
$F_{2}=i_{2}B_{1}l \qquad(1)$
The magnetic field due to conductor PQ is:
$B_{1}= \frac{\mu_{\circ}}{2\pi} \frac{i_{1}}{r}$
Now substitute the value of $B_{1}$ in equation $(1)$ so the force on conductor $RS$
$F_{2}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r}l $
So the force per unit length on the conductor $RS$ is
$\frac{F_{2}}{l}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r} \qquad(2)$
Similarly, we can solve the force per unit length on the conductor $PQ$
$\frac{F_{1}}{l}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r} \qquad(3)$
So from the above equation, we can conclude that the force per unit length is the same on both conductors whether both have different amounts of current flowing. The generalized form of the force per unit length from the above equations is
$\frac{F}{l}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r}$
Note: When both parallel conductors have the same direction of current then the force between the conductor will be repulsive. or when both parallel conductors have opposite directions of current then the force between the conductor is attractive.


