It is an arrangement of four resistance used to determine one of this resistance quickly and accurately in terms of the remaining three resistance.
Objective:
To find the unknown resistance with the help of the remaining three
resistance.
Principle of Wheatstone Bridge: The principle of Wheatstone bridge is based on the
principle of Kirchhoff's Law.
Construction:
A Wheatstone bridge consists of four resistance $P$,$Q$,$R$, and $S$. This resistance is connected to form quadrilateral $ABCD$. A battery of EMF $E$
is connected between point $A$ and $C$ and a sensitive galvanometer is connected
between point $B$ and $D$ Which is shown in the figure below.
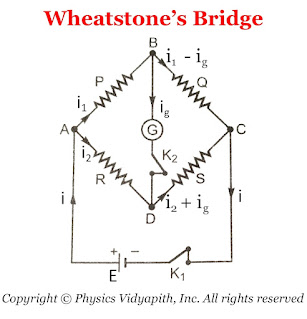 |
| Diagram of Wheatstone's Bridge |
Working:
To find the unknown resistance $S$, The resistance $R$ is to be adjusted
like there is no deflection in the galvanometer. which means that there is not
any flow of current in the arm $BD$. This condition is called "Balanced
Wheatstone bridge" i.e
$\frac{P}{Q}=\frac{R}{S}$
Derivation of Balanced Condition of Wheatstone's Bridge: In accordance with
Kirchhoff's first law, the currents through various branches are shown in the figure
above.
For Close Loop $ABDA$
$0=P \: I_{1} - R \: I_{2} +G \: I_{g} \qquad(1)$
For Close Loop $CBDC$
$0=Q \left( I_{1} - I_{g} \right) -S \left( I_{2} + I_{g} \right) - G\: I_{g}
\qquad(2)$
For Balanced Wheatstone Bridge: $I_{g}=0$
SO from equation $(1)$ and equation $(2)$
$0=P \: I_{1} - R \: I_{2} $
$P \: I_{1} = R \: I_{2} \qquad(3)$
$0=Q I_{1} -S I_{2}$
$Q I_{1} = S I_{2} \qquad(4)$
Now divide the equation $(4)$ and equation $(3)$, then we get
$\frac{P}{Q}=\frac{R}{S}$


