Derivation→
Let us consider
The length of the conductor = $l$
The cross-section area of the conductor = $A$
The total number of free electrons inside the conductor = $N$
The current flow in the conductor = $i$
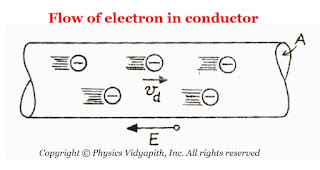 |
| The flow of Electron in Conductor |
The Relaxation time between the two successive collisions =$\tau$
According to the law of current density
$J=\frac{i} {A} $
$J=\frac{q} {A \tau} \qquad \left( \because i=\frac{q}{\tau} \right)$
$J=\frac{N \: e }{A \tau} \qquad \left( \because q=Ne \right)$
Now multiply by length of conductor $l$ in above equation. Therefore we get
$J=\frac{N \: e \: l}{A \tau\: l} $
$J=\frac{N \: e \: l}{V \tau\: }\qquad \left(\because V=A.l \right)$
Where $V$ is volume of the conductor.
$J=\frac{n \: e \: l}{ \tau }\qquad \left( \because n=\frac{N}{V} \right)$
Where $n$ is total number of electrons per unit .
$J=n \: e \: v_{d}\qquad \left( \because v_{d}=\frac{l}{\tau}\right)$
Where $v_{d}$ are known as drift velocity of charged particles.
Now substitute the value of current density $J$ from equation $(1)$ to above equation then above equation can be written as
$i=neAv_{d}$


