Angle of Acceptance →
If incident angle of light on the core for which the incident angle on the core-cladding interface equals the critical angle then incident angle of light on the core is called the "Angle of Acceptance.
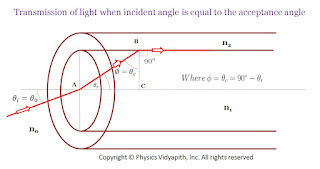 |
Transmission of light when the incident angle is equal to the acceptance angle
|
If the incident angle is greater than the acceptance angle i.e. $\theta_{i}>\theta_{0}$ then the angle of incidence on the core-cladding interface will be less than the critical angle due to which part of the incident light is transmitted into cladding as shown in the figure below
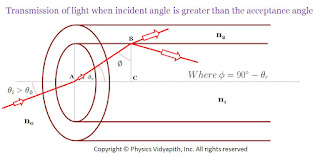 |
| Transmission of light when the incident angle is greater than the acceptance angle |
If the incident angle is less than the acceptance angle i.e. $\theta_{i}<\theta_{0}$ then the angle of incidence on the core-cladding interface will be greater than the critical angle for which total internal reflection takes place inside the core. As shown in the figure below
 |
| Transmission of light when the incident angle is less than the acceptance angle |
Acceptance cone →
The light entering the core in a cone of semi-vertical angle $\theta_{0}$ is transmitted in the core through total internal reflections. This cone is known as the acceptance cone.
Numerical Aperture→
The sine of the angle of acceptance of the optical fibre is known as the numerical aperture of optical fibre.
The numerical aperture determines the light-gathering ability of the fibre. It measures the amount of light that can be accepted by a fibre. The numerical aperture depends upon the refractive index of the core and cladding material and does not depend on the physical dimension of the fibre. It is a dimensionless quantity that is less than unity. The value of the numerical aperture ranges from $0.13$ to $0.15$. A large numerical aperture implies that a fibre accepts a large amount of light from the source. It varies due to variations of refractive index in the core and it has zero value after the core-cladding boundary. The number of propagation modes to multimode graded-index fibre depends upon the parameter of numerical aperture and hence upon the relative refractive index difference $\Delta n$
Derivation of Angle of Acceptance and Numerical Aperture →
Let us consider, step-index optical fibre for which
The incident angle on the axis of core = $\theta_{i}$
The refracted angle on the axis of core = $\theta_{r}$
The refractive index of core = $n_{1}$
The refractive index of cladding = $n_{2}$
The incident angle at the core-cladding interface = $\phi$.
 |
Transmission of light when the incident angle is equal to the acceptance angle
|
When ray incident at point $A$ on the core then According to Snell's law
$\frac{sin \theta_{0}}{sin \theta_{r}}= \frac{n_{1}}{n_{0}} $
Where $n_{0}$ → refractive index of air and vacuum
$sin\theta_{0}=\frac{n_{1}}{n_{0}} sin \theta_{r} \qquad(1)$
Now the refracted ray incident at point $B$ at the interface of core and cladding. So for critical angle condition
$n_{1}\: sin\phi=n_{2} \: sin90^{0} $
$n_{1}\: sin(90-\theta_{r})=n_{2} \: sin90^{0} \qquad (\because \phi=90-\theta_{r})$
$n_{1}\: cos \theta_{r}=n_{2}$
$cos\theta_{r}=\frac{n_{2}}{n_{1}} \qquad(2)$
$sin\theta_{r}=\sqrt{1-cos^{2}\theta_{r}}$
Now substitue the value of $cos\theta_{r}$ from equation$(2)$ to above equation then we get
$sin\theta_{r}=\sqrt{1- \left ( \frac{n_{2}}{n_{1}} \right)^{2}}$
$sin\theta_{r}=\frac{1}{n_{1}}\sqrt{n_{1}^{2}- n_{2}^{2}}$
Now substitue the value of $sin\theta_{r}$ in equation$(1)$ then we get
$sin\theta_{0}=\frac{n_{1}}{n_{0}}\frac{1}{n_{1}}\sqrt{n_{1}^{2}- n_{2}^{2}}$
$sin\theta_{0}=\frac{\sqrt{n_{1}^{2}- n_{2}^{2}}}{n_{0}}\qquad(3)$
This $sin\theta_{0}$ is known as Numerical Aperture. i.e.
$N.A.=\frac{\sqrt{n_{1}^{2}- n_{2}^{2}}}{n_{0}}$
If fibre is in the air then $n_{0}=1$ so the above equation can be written as
$N.A.=\sqrt{n_{1}^{2}- n_{2}^{2}}$
The equation $(3)$ also can be written as
$\theta_{0}=sin^{-1}\frac{\sqrt{n_{1}^{2}- n_{2}^{2}}}{n_{0}}$
The angle $\theta_{0}$ is known as the Angle of Acceptance.
The light is transmitted through the fibre when
$\theta_{i} < \theta_{0}$
i.e. $sin \theta_{i} < sin \theta_{0}$
$sin \theta_{i} < N.A.$
The light will be transmitted through the fibre with multiple total internal reflections when the above condition is satisfied.




