Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below.
 |
Particle in One-Dimensional Box(Infinite Potential Well) |
The potential energy inside the one -dimensional box can be represented as
$\begin{Bmatrix}
V(x)=0 &for \: 0\leq x \leq L \\
V(x)=\infty & for \: 0> x > L \\
\end{Bmatrix}$
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$
If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as:
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{8 \pi^{2} mE}{h^{2}}\psi(x)=0 \quad (\because \hbar=\frac{h}{2 \pi}) \quad(2)$
$\frac{d^{2} \psi(x)}{d x^{2}}+ k^{2}\psi(x)=0 \quad (\because k^{2}=\frac{8 \pi^{2} mE}{h^{2}}) \quad(3)$
The general solution of the above differential equation $(2)$
$\psi(x)= A sin(kx)+ B cos(kx) \qquad(4)$
The wave function $\psi(x)$ should be zero everywhere outside the box since the probability of finding the particle outside the box is zero. Similarly, the wave function $\psi(x)$ must also be zero at walls of the box because the probability density $[\psi(x)]^{2}$ must be continuous. Thus, the boundary conditions for this problem is that
(i) $\psi(x)=0$ For $x=0$
(ii) $\psi(x)=0$ For $x=L$
Now applying the boundary condition in equation$(4)$ i.e.
(i) At $x=0$ the wave function $\psi(0)=0$
Now we get
$\psi(0)= A sin(k.0)+ B cos(k.0)$
$A sin(k.0)+ B cos(k.0)=0 \qquad (\because \psi(0)= 0)$
$B=0$
Hence substitute the value of $B$ in equation$(4)$ ,
$\psi(L)= A sin(kx) \qquad(5)$
Now applying the second boundary condition:
(ii) At $x=L$ the wave function $\psi(L)=0$, we get
$\psi(x)= A sin(kL) \qquad(6)$
This equation will satisfy only for certain values of $k$, say $k_{n}$. Since $A$ can not be taken zero hence
$sin(k_{n}L)=0 $
$sin(k_{n}L)=sin(n\pi) $
$k_{n}L=n\pi $
$k_{n}=\frac{n\pi}{L} \qquad(7)$
Thus for each allowed values of $k_{n}$ there is a wave function $\psi(x)$ given as, using equation$(5)$ and equation$(7)$
$\psi_{n}(x)=A sin(\frac{n\pi x}{L})$
This is the expression of the wave function or eigen function for a particle in a box.
Now, from equation $(3)$ and equation$(7)$, we get
$k^{2}=\frac{8 \pi^{2} mE}{h^{2}}= (\frac{n \pi}{L})^{2}$
$E=\frac{n^{2} h^{2}}{8mL^{2}}$
This is the expression of energy or eigen value for a particle in a box.
In general, the expression for this energy is written as:
$E_{n}=\frac{n^{2} h^{2}}{8mL^{2}}$
For different values of $n$ energy values can be written as
For $n=1$
$E_{1}=\frac{h^{2}}{8mL^{2}}$
It is known as zero-point energy or ground energy state
For $n=2$
$E_{2}=\frac{2^{2} h^{2}}{8mL^{2}}=2^{2}E_{1}$
For $n=3$
$E_{3}=\frac{3^{2} h^{2}}{8mL^{2}}=3^{2}E_{1}$
For $n=4$
$E_{4}=\frac{4^{2} h^{2}}{8mL^{2}}=4^{2}E_{1}$
So generalized form of the above equation can be written as
$E_{n}=n^{2}E_{1}$
Some of the possible energies for a particle in a box are shown on an energy-level diagram in the figure below.
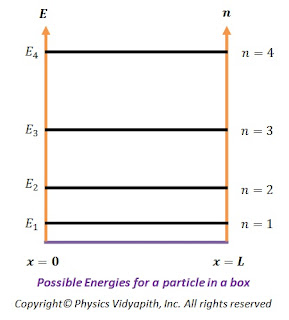 |
Possible Energies for a particle in a box |
The energy levels have a spacing that increases with increasing $n$ and thus the particle in a box can take only certain discrete energy values, called Eigen-values. This means that the energy levels of a particle in a box are quantized but according to classical mechanics, the particle may take any continuous range of energy values between zero and infinity.



